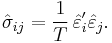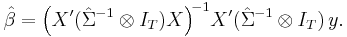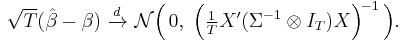Seemingly unrelated regressions
In econometrics, the seemingly unrelated regressions (SUR)[1] or seemingly unrelated regression equations (SURE)[2] model, proposed by Arnold Zellner in (1962), is a generalization of a linear regression model that consists of several regression equations, each having its own dependent variable and potentially different sets of exogenous explanatory variables. Each equation is a valid linear regression on its own and can be estimated separately, which is why the system is called seemingly unrelated,[3] although some authors[4] suggest that the term seemingly related would be more appropriate, since the error terms are assumed to be correlated across the equations.
The model can be estimated equation-by-equation using standard ordinary least squares (OLS). Such estimates are consistent, however generally not as efficient as the SUR method, which amounts to feasible generalized least squares with a specific form of the variance-covariance matrix. Two important cases when SUR is in fact equivalent to OLS, are: either when the error terms are in fact uncorrelated between the equations (so that they are truly unrelated), or when each equation contains exactly the same set of regressors on the right-hand-side.
The SUR model can be viewed as either the simplification of the general linear model where certain coefficients in matrix Β are restricted to be equal to zero, or as the generalization of the general linear model where the regressors on the right-hand-side are allowed to be different in each equation. The SUR model can be further generalized into the simultaneous equations model, where the right-hand side regressors are allowed to be the endogenous variables as well.
Contents |
The model
Suppose there are m regression equations
Here i represents the equation number, and t = 1, …, T is the observation index. The number of observations is assumed to be large, so that in the analysis we take T → ∞, whereas the number of equations m remains fixed.
Each equation i has a single response variable yit, and a ki-dimensional vector of regressors xit. If we stack observations corresponding to the i-th equation into T-dimensional vectors and matrices, then the model can be written in vector form as
where yi and εi are T×1 vectors, Xi is a T×ki matrix, and βi is a ki×1 vector.
Finally, if we stack these m vector equations on top of each other, the system will take form [5]
-
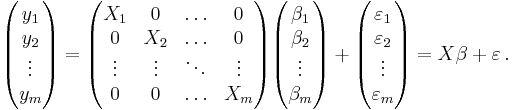
(
The assumption of the model is that error terms εit are independent across time, but may have cross-equation contemporaneous correlations. Thus we assume that E[ εit εjs | X ] = 0 whenever t ≠ s, whereas E[ εit εjt | X ] = σij. Denoting Σ = [[σij]] the m×m skedasticity matrix of each observation, the covariance matrix of the stacked error terms ε will be equal to [6]
where IT is the T-dimensional identity matrix and ⊗ denotes the matrix Kronecker product.
Estimation
The SUR model is usually estimated using the feasible generalized least squares (FGLS) method. This is a two-step method where in the first step we run ordinary least squares regression for (1). The residuals from this regression are used to estimate the elements of matrix Σ: [7]
In the second step we run generalized least squares regression for (1) using the variance matrix 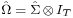 :
:
This estimator is unbiased in small samples assuming the error terms εit have symmetric distribution; in large samples it is consistent and asymptotically normal with limiting distribution [7]
Other estimation techniques besides FGLS were suggested for SUR model: the maximum likelihood (ML) method under the assumption that the errors are normally distributed; the iterative generalized least squares (IGLS), were the residuals from the second step of FGLS are used to recalculate the matrix 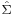 , then estimate
, then estimate 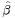 again using GLS, and so on, until convergence is achieved; the iterative ordinary least squates (IOLS) scheme, where estimation is performed on equation-by-equation basis, but every equation includes as additional regressors the residuals from the previously estimated equations in order to account for the cross-equation correlations, the estimation is run iteratively until convergence is achieved. Kmenta & Gilbert (1968) ran a Monte-Carlo study and established that all three methods — IGLS, IOLS and ML — yield the numerically equivalent results, they also found that the asymptotic distribution of these estimators is the same as the distribution of the FGLS estimator, whereas in small samples neither of the estimators was more superior than the others.
again using GLS, and so on, until convergence is achieved; the iterative ordinary least squates (IOLS) scheme, where estimation is performed on equation-by-equation basis, but every equation includes as additional regressors the residuals from the previously estimated equations in order to account for the cross-equation correlations, the estimation is run iteratively until convergence is achieved. Kmenta & Gilbert (1968) ran a Monte-Carlo study and established that all three methods — IGLS, IOLS and ML — yield the numerically equivalent results, they also found that the asymptotic distribution of these estimators is the same as the distribution of the FGLS estimator, whereas in small samples neither of the estimators was more superior than the others.
Equivalence to OLS
There are two important cases when the SUR estimates turn out to be equivalent to the equation-by-equation OLS, so that there is no gain in estimating the system jointly. These cases are:
- When the matrix Σ is known to be diagonal, that is, there are no cross-equation correlations between the error terms. In this case the system becomes not seemingly but truly unrelated.
- When each equation contains exactly the same set of regressors, that is X1 = X2 = … = Xm. That the estimators turn out to be numerically identical to OLS estimates follows from Kruskal's theorem,[8] or can be shown via the direct calculation.[9]
See also
Notes
- ^ Davidson & MacKinnon (1993, page 306), Hayashi (2000, page 279), Greene (2002, p. 340)
- ^ Zellner (1962), Srivastava & Giles (1987, page 2)
- ^ Greene (2002, p. 342)
- ^ Davidson & MacKinnon (1993, page 306)
- ^ Zellner (1962, eq. (2.2))
- ^ Zellner (1962, eq. (2.4)), Greene (2002, p. 342)
- ^ a b Amemiya (1985, page 198)
- ^ Davidson & MacKinnon (1993, page 313)
- ^ Amemiya (1985, page 197)
References
- Amemiya, Takeshi (1985). Advanced econometrics. Cambridge, Massachusetts: Harvard University Press. ISBN 0-674-00560-0.
- Davidson, Russell; MacKinnon, James G. (1993). Estimation and inference in econometrics. Oxford University Press. ISBN 978-0-19-506011-9.
- Greene, William H. (2002). Econometric analysis (5th ed.). Prentice Hall. ISBN 0-13-066198-9.
- Hayashi, Fumio (2000). Econometrics. Princeton University Press. ISBN 0-691-01018-8.
- Kmenta, Jan; Gilbert, Roy F. (1968). "Small sample properties of alternative estimators of seemingly unrelated regressions". Journal of the American Statistical Association 63 (324): 1180–1200. doi:10.2307/2285876.
- Srivastava, Virendra K.; Giles, David E.A. (1987). Seemingly unrelated regression equations models: estimation and inference. New York: Marcel Dekker. ISBN 978-0-82-477610-7.
- Zellner, Arnold (1962). "An efficient method of estimating seemingly unrelated regression equations and tests for aggregation bias". Journal of the American Statistical Association 57: 348–368. doi:10.2307/2281644.
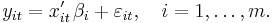
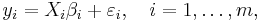
![\Omega \equiv \operatorname{E}[\,\varepsilon\varepsilon'\,|X\,] = \Sigma \otimes I_T,](/2012-wikipedia_en_all_nopic_01_2012/I/186e0fca788bcc4fe42b0b6ea302d855.png)